 【 微信掃碼咨詢(xún) 】
【 微信掃碼咨詢(xún) 】

六自由度平臺(tái)的運(yùn)動(dòng)學(xué)和動(dòng)力學(xué)是各國(guó)學(xué)者競(jìng)相研究的兩大領(lǐng)域。并聯(lián)機(jī)構(gòu)動(dòng)力學(xué)的問(wèn)題十分復(fù)雜,導(dǎo)致取得的相關(guān)理論成果較少。研究六自由度平臺(tái)各支腿力矩與負(fù)載平臺(tái)的關(guān)系,就必須對(duì)其建立動(dòng)力學(xué)模型。
數(shù)學(xué)建模是研究空間問(wèn)題常用的方法之一,通過(guò)建立模型可以對(duì)抽象的問(wèn)題作定量的分析,方便研究。運(yùn)用Newton-Eulr法建立了六自由度平臺(tái)的動(dòng)力學(xué)模型,并應(yīng)用Matlab編寫(xiě)動(dòng)力學(xué)力矩算法并進(jìn)行仿真,對(duì)六自由度平臺(tái)的動(dòng)力學(xué)進(jìn)行了具體的分析。
牛頓-歐拉動(dòng)力學(xué)方程
我們假設(shè)六自由度平臺(tái)的每個(gè)部件都為剛體,只有給剛體一個(gè)加速度或減速度才能使剛體運(yùn)動(dòng),但產(chǎn)生加速度就必須給剛體相應(yīng)的力,而這個(gè)力又是關(guān)于加速度和剛體質(zhì)量分布的函數(shù),也就是有一個(gè)在一定條件下可以相互轉(zhuǎn)換的關(guān)系。為了得出它們之間的函數(shù)關(guān)系,可以利用牛頓方程和歐拉公式,經(jīng)過(guò)推導(dǎo)即可得出平臺(tái)各支腿驅(qū)動(dòng)力矩、負(fù)載力、慣量和加速度之間的關(guān)系。
在利用牛頓方程和歐拉公式進(jìn)行動(dòng)力學(xué)方程推導(dǎo)前,我們先分析下轉(zhuǎn)動(dòng)慣量的計(jì)算。轉(zhuǎn)動(dòng)慣量的定義是剛體在轉(zhuǎn)動(dòng)時(shí)候會(huì)產(chǎn)生一個(gè)慣性,把這個(gè)慣性作一個(gè)定量的表示。轉(zhuǎn)動(dòng)慣量在后邊求取六自由度平臺(tái)支腿角速度,角加速度和力矩時(shí)都會(huì)用到。
如下圖所示,可以得到剛體在坐標(biāo)系 下的慣量矩陣為:
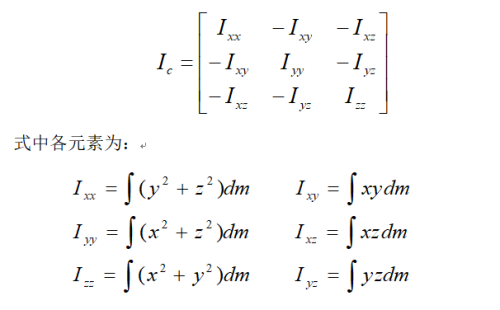
由于在下面動(dòng)力學(xué)方程的推導(dǎo)過(guò)程中也會(huì)用到平行軸定理,在這里就簡(jiǎn)單的介紹一下。首先在上面得出了剛體于坐標(biāo)系下的慣量張量,平行軸定理指的是計(jì)算坐標(biāo)系平移時(shí)剛體慣性張量的方法。下面給出坐標(biāo)平移后相對(duì)于坐標(biāo)系{A}的慣性張量為:
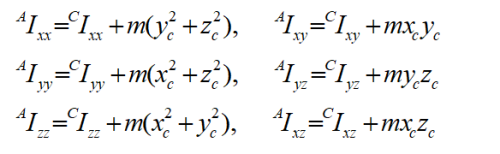
以上是對(duì)六自由度平臺(tái)剛體質(zhì)量分布做的簡(jiǎn)單的分析,給出了慣性矩陣方程以及平行軸定理的表達(dá)式。基于這些前期工作的準(zhǔn)備,下面對(duì)牛頓—?dú)W拉方程進(jìn)行闡述。首先對(duì)質(zhì)心的平動(dòng)進(jìn)行研究,如上圖所示, 表示質(zhì)心處的位置,那么質(zhì)心處的加速度為 ;在繞質(zhì)心的轉(zhuǎn)動(dòng)分析過(guò)程中,假設(shè)剛體轉(zhuǎn)動(dòng)的角速度,則令表示角加速度,則可以得出作用在剛體質(zhì)心 處的力和力矩方程為:
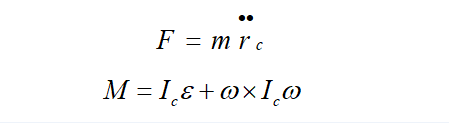
 網(wǎng)站二維碼
網(wǎng)站二維碼
 微信二維碼
微信二維碼
網(wǎng)站地圖 蘇州通諾爾智能科技有限公司 版權(quán)所有 2008-2021 蘇ICP備2021049911號(hào)